条件随机场

另一种常用模型为条件随机场(CRF)模型,条件随机场是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔可夫随机场。本章节按照以下几部分组织：

• 概率无向图模型
• 条件随机场定义与形式
• 条件随机场概率计算
• 条件随机场学习算法
• 条件随机场预测算法

概率无向图模型

概率无向图模型定义

图是由节点和及连接的边组成的集合，表示为$G = (V,E)$，若连接的边无方向，则称为无向图，反之则称为有向图。
概率图模型是由图表示的概率分布，图中的节点表示随机变量，节点之间的边表示变量之间的概率依赖关系。
给定一个联合概率分布$P(Y)$和表示它的无向图$G$,首先定义无向图表示的随机变量之间存在的成对马尔可夫性、局部马尔可夫性和全局马尔可夫性。

• 成对马尔可夫性：设$\mu$和$v$是无向图$G$中任意两个没有边连接的节点，两个节点分别对应随机变量$Y{\mu},Y_v$。其他所有节点的集合记做$O$,对应随机变量组是$Y_O$。成对马尔可夫性是指给定随机变量组$Y_O$的条件下，随机变量$Y{\mu}$和$Y_v$是条件独立的,即： $$P(Y_{\mu},Y_v|Y_O) = P(Y_{\mu}|Y_O)P(Y_{v}|Y_O)$$
• 局部马尔可夫性：设$v \in V$是无向图$G$中任意一个节点，$W$是与$v$有边连接的所有节点，$O$是$v$和$W$以外的其他所有节点。$v,W,O$对应的随机变量(组)记做$Y_v,Y_W,Y_O$,局部马尔可夫性是指在给定随机变量组$Y_W$条件下，随机变量$Y_v$与随机变量组$Y_O$是相互独立的: $$P(Y_{O},Y_v|Y_W) = P(Y_{v}|Y_W)P(Y_{O}|Y_W)$$ 在$P(Y_O|Y_W)>0$情况下，有： $$P(Y_v|Y_W) = P(Y_v|Y_W,Y_O)$$
• 全局马尔可夫性：设结点集合$A,B$是在无向图$G$中被节点集合$C$分开的任意节点集合，它们所对应的变量组记做$Y_A,Y_B,Y_C$。全局马尔可夫性是指给定随机变量组$Y_C$条件下随机变量组$Y_A，Y_B$是条件独立的，即： $$P(Y_A,Y_B|Y_C) = P(Y_A|Y_C)P(Y_B|Y_C)$$

下面定义概率无向图模型:

概率无向图模型: 设有联合概率分布$P(Y)$，由无向图$G = (V,E)$表示，在图$G$中，节点表示随机变量，边表示随机变量之间的概率依赖关系。若联合概率分布$P(Y)$满足成对、局部或全局马尔可夫性,就称此概率分布为概率无向图模型，或马尔可夫随机场。

概率无向图模型的因子分解

能够使用图模型来对联合概率分布进行编码，主要出发点便是变量之间的马尔可夫性假设，这让我们可以以更加紧凑的形式来表示联合概率分布。
首先给出无向图中团与最大团的定义:

团与最大团:无向图中任何两个节点均有边连接的子集称为团(clique)。若$C$是无向图$G$的一个团，并且不能够再加入任何一个$G$的节点使其成为一个更大的团，则称此$C$为最大团。

将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积的操作，称为概率无向图模型的因子分解。
给定概率图模型，设其无向图为$G$，$C$为$G$上的最大团，$Y_C$表示$C$对应的随机变量，那么联合概率分布$P(Y)$可以表示成图中所有最大团$C$上函数$\varPhi_C(Y_C)$的连乘形式:

$$P(Y) = \frac{1}{Z} \prod_{C} \varPhi_C(Y_C)$$

公式中$Z$是一个归一化因子$Z = \sumY \prod{C} \varPhi_C(Y_C)$。函数$\varPhi_C(Y_C)$称为势函数。势函数通常定义为指数函数:

$$\varPhi_C(Y_C) = exp\{ -E(Y_C)\}$$

概率无向图的因子分解由Hammersley-Clifford定理保证:

Hammersley-Clifford定理: 概率无向图模型的联合概率分布$P(Y)$可以表示为如下形式:

$$P(Y) = \frac{1}{Z} \prod_C \varPhi_C(Y_C)$$

其中，$C$是无向图的最大团，$Y_C$是$C$的节点对应的随机变量，$\varPhi_C(Y_C)$是$C$上定义的严格正函数，乘积是在无向图所有的最大团上进行的，关于该定理的证明参考链接Hammersley-Clifford定理证明

条件随机场的定义与形式

条件随机场的定义

条件随机场是给定随机变量$X$条件下，随机变量$Y$的马尔可夫随机场。本文主要介绍线性链条件随机场，该模型可用于标注等问题。这时，在条件概率模型$P(Y|X)$中，$Y$是输出变量，表示标记序列(状态序列)，$X$是输入变量，表示需要标注的观测序列。学习时，利用训练数据集通过极大似然估计或正则化的极大似然估计得到条件概率模型$\hat{P}(Y|X)$;预测时，对于给定的输入序列$x$,求出条件概率$\hat{P}(y|x)$最大的输出序列$\hat{y}$。
首先给出一般的条件随机场的定义:

条件随机场：设$X$和$Y$是随机变量，$P(Y|X)$是在给定$X$条件下$Y$的条件概率分布。若随机变量$Y$构成一个由无向图$G = (V,E)$表示的马尔可夫随机场，即：

$$P(Y_v|X,Y_w,w \neq v) = P(Y_v|X,Y_w,w\sim v)$$

对任意节点$v$成立，则称条件概率分布$P(Y|X)$为条件随机场。公式中$w \sim v$表示在图$G = (V,E)$中与节点$v$有边连接的所有节点$w$,$w \neq v$表示节点$v$以外的所有节点，$Yv,Y_w,Y{\mu}$为节点$v,\mu,w$所对应的随机变量。

虽然在定义中并没有要求$X$和$Y$具有相同的结构，但在现实中，一般假设$X$和$Y$具有相同的结构，而对于线性链，则是图$G = (V,E)$可以表示成：

$$G = (V = \{ 1,2,\dots,n\}, E = \{(i,i+1)\}),\quad i = 1,2,\dots,n-1$$

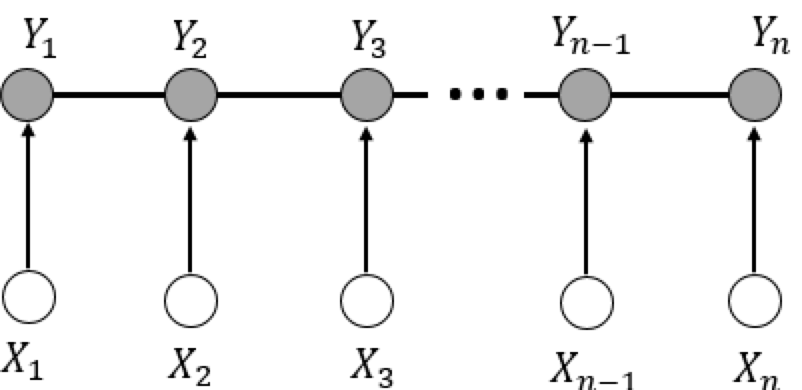
下面给出线性链条件随机场的定义：

线性链条件随机场：设$X = (X_1,X_2,\dots,X_n),Y= (Y_1,Y_2,\dots,Y_n)$均为线性链表示的随机变量序列，若在给定随机变量序列$X$的条件下，随机变量序列$Y$的条件概率分布$P(Y|X)$构成条件随机场，即满足马尔可夫性：

$$P(Y_i|X,Y_1,\dots,Y_{i-1},Y_{i+1},\dots,Y_n) = P(Y_i|X,Y_{i-1},Y_{i+1}),i =1,\dots,n$$

则称$P(Y|X)$为线性链条件随机场。在标注问题中，$X$表示输入观测序列，$Y$表示对应的输出标记序列或状态序列。

条件随机场的参数化形式

下面给出条件随机场的参数化形式：
线性链条件随机场参数化形式：设$P(Y|X)$为线性链条件随机场，则在随机变量$X$取值为$x$条件下，随机变量$Y$取值为$y$的条件概率具有如下形式:

$$P(y|x) = \frac{1}{Z(x)} exp(\sum_{i,k} \lambda_k t_k(y_{i-1},y_i,x,i) + \sum_{i,l} \mu_l s_l(y_i,x,i) )$$

其中$Z(x)$为归一化因子，保证$P(y|x)$满足概率形式，$t_k$和$s_l$是特征函数，$\lambda_k$和$\mu_l$是对应的权值。

定义中公式表示给定输入序列$x$，对输出序列$y$预测的条件概率。$t_k$是定义在边上的特征函数，称为转移特征，依赖于当前和前一个位置；$s_l$是定义在节点上的特征函数，称为状态特征，依赖于当前位置。$t_k$和$s_l$都依赖于位置，是局部特征函数。通常，特征函数$t_k$和$s_l$取值为0或1，当满足特征条件时取值为1，否则为0。条件随机场完全由特征函数$t_k,s_l$和对应的权值$\lambda_k,\mu_l$确定。
为便于理解，下面给出一个线性链条件随机场的栗子：

🌰： 设有一标注问题：输入观测序列为$X = (X_1,X_2,X_3)$,输出标记序列为$Y = (Y_1,Y_2,Y_3)$,输出标记取之于$\mathcal{Y} = { 1,2 }$
假设特征$t_k,s_l$和对应的权值$\lambda_k,\mu_l$如下：

$$\begin{aligned} t_1 &= t_1(y_{i-1} = 1,y_i = 2,x,i) \quad i =2,3, \lambda_1 = 1 \\ t_2 &= t_2(y_1 = 1,y_2 = 1,x,2),\quad \lambda_2 = 0.6 \\ t_3 &= t_3(y_2 = 2,y_3 =1,x,3), \quad \lambda_3 = 1 \\ t_4 &= t_4(y_1 = 2,y_2 = 1,x,2), \quad \lambda_4 = 1 \\ t_5 &= t_5(y_2 = 2,y_3 =2,x,3),\quad \lambda_5 = 0.2 \\ s_1 &= s_1(y_1 = 1,x,1), \qquad \qquad \mu_1 = 1 \\ s_2 &= s_2(y_i =2,x,i),i =1,2 \quad \mu_2 = 0.5 \\ s_3 &= s_3(y_i =1,x,i),i =1,2 \quad \mu_2 = 0.8 \\ s_4 &= s_4(y_3 =2,x,3),i =1,2 \quad \mu_2 = 0.5 \end{aligned}$$

对于给定的观测序列，求标记序列为$y = (y_1,y_2,y_3) = (1,2,2)$的非规范条件概率(不进行归一化)
解：由线性链条件随机场的参数化形式可得:

$$P(y_1 = 1,y_2 = 2,y_3 =2|x) \propto exp(3.2)$$

条件随机场的简化形式

注意到条件随机场的参数化形式中同一特征在各个位置都有定义，因此可以考虑对同一个特征在各个位置求和，将局部特征函数转化成一个全局特征函数，这样就可以将条件随机场写成权值向量和特征向量的内积形式，即条件随机场的简化形式。
假设有$K_1$个转移特征，$K_2$个状态特征，$K = K_1 + K_2$,记：

$$f_k(y_{i-1},y_i,x,i) = \begin{cases} t_k(y_{i-1},y_i,x,i), & k =1,2,\dots,K_1 \\ s_l(y_i,x,i), & k = K_1 + l; l = 1,2,\dots,K_2 \end{cases}$$

然后对转移与状态特征在各个位置$i$求和，记做：

$$f_k(y,x) = \sum_{i=1}^n f_k(y_{i-1},y_i, x,i),\quad k = 1,2,\dots,K$$

用$w_k$表示特征$f_k(y,x)$的权值，即：

$$w_k = \begin{cases} \lambda_k, & k =1,2,\dots, K_1 \\ \mu_l , & k = K_1 + l; l= 1,2,\dots,K_2 \end{cases}$$

于是条件随机场参数化可以写成更加紧凑的形式：

$$\begin{aligned} P(y|x) &= \frac{1}{Z(x)} exp \sum_{k=1}^K w_k f_k(y,x) \\ Z(x) &= \sum_y exp \sum_{k=1}^K w_k f_k(y,x) \end{aligned}$$

若以$\boldsymbol{w}$表示权值向量，即：

$$\boldsymbol{w} = (w_1,w_2,\dots,w_K)^T$$

以$\boldsymbol{F(y,x)}$表示全局特征向量:

$$\boldsymbol{F(y,x)} = (f_1(y,x),f_2(y,x),\dots, f_K(y,x))^T$$

则条件随机场可以以两个向量内积的形式来表示:

$$P_w(y|x) = \frac{exp(\boldsymbol{w \cdot F(y,x)})}{Z_w(x)}$$

条件随机场的矩阵形式

假设$Pw(y|x)$是线性链条件随机场，表示对给定观测序列，相应的标记序列$y$的条件概率。对每个标记序列引入特殊的起点和终点状态标记$y_0 = start$和$y{n+1} = stop$,这时标注序列的概率可以通过矩阵形式表示并有效计算。
对观测序列$x$的每一个位置$i =1,2,\dots,n+1$,由于$y_{i-1}$和$y_i$在$m$个标记中取值，因此可以定义一个$m$阶矩阵随机变量：

$$M_i(x) = [M_i(y_{i-1},y_i|x)]$$

矩阵随机变量元素为:

$$\begin{aligned} M_i(y_{i-1},y_i|x) &= exp(W_i(y_{i-1},y_i|x)) \\ W_i(y_{i-1},y_i|x) &= \sum_{k=1}^K w_k f_k(y_{i-1},y_i,x,i) \end{aligned}$$

这样，给定观测序列$x$,相应的标记序列$y$的非规范概率可以通过该序列$n+1$个矩阵的适当元素的乘积
$\prod{i=1}^{n+1} M_i(y{i-1},y_i|x)$,于是，条件概率$P_w(y|x)$可以表示为：

$$P_w(y|x) = \frac{1}{Z_w(x)} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x)$$

其中$Zw(x) = \sum_y \prod{i=1}^{n+1} Mi(y{i-1},y_i|x)$,可以证明，该归一化因子也可以表示成$n+1$个矩阵连乘积的矩阵的元素。
下面的部分依次介绍条件随机场的三个经典问题：

• 概率计算问题，即给点条件随机场$P(Y|X)$,输入序列$x$和输出序列$y$,计算相应条件概率的问题
• 学习问题，即在给定训练数据集情况下估计条件随机场模型参数的问题
• 预测问题，即在给定条件随机场$P(Y|X)$和输入序列$x$,求条件概率最大的输出序列$y^*$,即对观测序列进行标注。

概率计算问题比较简单，也是后两个问题的基础，而在实际进行应用中，我们首先需要明确线性链条件随机场是否适用于待解决的问题，然后利用已有的训练数据来进行模型学习，最终再用学习得到的模型进行预测(标注)。

条件随机场概率计算问题

与隐马尔可夫模型的概率计算类似，对于这种有明显前后关联的概率模型， 往往都是采用递推方式来进行概率计算，通过引入前向-后向向量，递归地进行概率计算，该算法也被称为前向-后向算法。

前向-后向算法

对每个指标$ i =0,1,\dots,n+1$,定义前向向量$\alpha_i(x)$:

$$\alpha_0(y|x) = \begin{cases} 1, &y = start \\ 0, & other \end{cases}$$

递推公式为:

$$\alpha_i^T(y_i|x) = \alpha_{i-1}^T(y_{i-1}|x)[M_i(y_{i-1},y_i|x)],\quad i = 1,2,\dots,n+1$$

也可表示为：

$$\alpha_i^T(x) = \alpha_{i-1}^T(x) M_i(x)$$

$\alphai(y_i|x)$表示在位置$i$的标记是$y_i$，并且从1到$i$的前部分标记序列的非规范化概率，$y_i$可以取的值有$m$个，在上述公式中，$\alpha{i-1}(x)$是一个$m$维列向量，而$Mi(x)$是一个$m$阶矩阵，实际上$y_i$的任意取值均可能由$y{n-1}$的$m$种状态转移过来，因此上述的计算实际上是对各种转移可能性的求和。
同样，对每个指标$i = 0,1,\dots,n+1$,定义后向向量$\beta_i(x)$:

$$\begin{aligned} \beta_{n+1}(y_{n+1|x}) &= \begin{cases} 1, & y_{n+1} = stop \\ 0, & other \end{cases} \\ \beta_i(y_i|x) &= [M_{i+1}(y_i,y_{i+1}|x)] \beta_{i+1}(y_{i+1}|x) \end{aligned}$$

又可表示为：

$$\beta_i(x) = M_{i+1}(x) \beta_{i+1}(x)$$

$\beta_i(y_i|x)$表示在位置$i$的标记为$y_i$并且从$i+1$到$n$后半部分标记序列的非规范化序列。

概率计算

按照前向后向概率的定义，很容易计算标记序列在位置$i$是标记$yi$的条件概率和在位置$i-1$和$i$是标记$y{i-1}$和$y_i$的条件概率：

$$\begin{aligned} P(Y_i = y_i|x) &= \frac{\alpha_i^T(y_i|x) \beta_i(y_i|x)}{Z(x)} \\ P(Y_{i-1} = y_{i-1},Y_i = y_i|x) &= \frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x) \beta_i(y_i|x)}{Z(x)} \end{aligned}$$

其中，

$$Z(x) = \alpha_n^T(x) \boldsymbol{1} = \boldsymbol{1} \beta_1(x)$$

$\boldsymbol{1}$是元素全为1的$m$维列向量

期望值计算

利用前向、后向向量，可以计算特征函数关于联合分布$P(X,Y)$和条件分布$P(Y|X)$的数学期望。
特征函数$f_k$关于条件分布$P(Y|X)$的数学期望是:

$$\begin{aligned} E_{P(Y|X)}[f_k] &= \sum_y P(y|x) f_k(y,x) \\ &= \sum_{i=1}^{n+1} \sum_{y_{i-1},y_i} f_k(y_{i-1},y_i,x,i) P(Y_{i-1} = y_{i-1},Y_i = y_i|x) \\ &\qquad k = 1,2,\dots,K \end{aligned}$$

能够这样进行展开，实际上还是从$f_k(y,x)$的定义出发：

$$f_k(y,x) = \sum_{i=1}^{n+1} f_k(y_{i-1},y_i, x,i),\quad k = 1,2,\dots,K$$

展开之后便是上述形式，这中写法也显示了在概率图中，联合概率分布可以表示成一系列局部概率分布的乘积形式。
假设经验分布为$\tilde{P}(X)$,则特征函数关于联合分布$P(X,Y)$的数学期望可以表示为：

$$\begin{aligned} E_{P(X,Y)}[f_k] &= \sum_{x,y}P(x,y) \sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i) \\ &= \sum_{x} \tilde{P}(x) \sum_{i=1}^{n+1} \sum_{y_{i-1},y_i} f_k(y_{i-1},y_i,x,i) P(Y_{i-1} = y_{i-1},Y_i = y_i|x) \\ &\quad, i =1,2,\dots,K \end{aligned}$$

有了前向、后向算法，对于给定的观测序列$x$与标记序列$y$，可以通过一次前向扫描计算$\alpha_i$及$Z(x)$,通过一次后向扫描计算$\beta_i$,从而计算所有的概率和特征的期望。

条件随机场的学习算法

条件随机场模型实际上是定义在时序数据上的对数线性模型，其学习方法包括极大似然估计和正则化的极大似然估计，具体的优化实现算法有改进的迭代尺度法IIS、梯度下降法及拟牛顿法。

改进的迭代尺度法

已知训练数据集，由此可知经验概率分布$\tilde{P}(X,Y)$，可以通过极大化训练数据的对数似然函数来求模型参数。
训练数据的对数似然函数为:

$$\begin{aligned} L(w) &= L_{\tilde{P}}(P_w) = \log \prod_{x,y} P_w(y|x)^{\tilde{P}(x,y)} = \sum_{x,y} \tilde{P}(x,y) \log P_w(y|x) \\ &= \sum_{x,y} [\tilde{P}(x,y) \sum_{k=1}^K w_k f_k(y|x) -\tilde{P}(x,y) \log Z_w(x)] \\ &= \sum_{j=1}^N \sum_{k=1}^K w_k f_k(y_j,x_j) - \sum_{j=1}^N \log Z_w(x_j) \end{aligned}$$

这一部分先挖坑，等我补一下相关知识再来填坑……..

条件随机场预测算法

条件随机场的预测问题是指给定条件随机场$P(Y|X)$和输入序列(观测序列)$x$,求条件概率最大的输出序列$y^*$,即对观测序列进行标注。与HMM模型中的预测问题类似，该问题可以通过维特比算法进行解决。
由条件随机场的简化形式:

$$P_w(y|x) = \frac{exp(\boldsymbol{w \cdot F(y,x)})}{Z_w(x)}$$

可知：

$$\begin{aligned} y^* &= \arg \max_{y} P_w(y|x) \\ &= \arg \max_{y} \frac{exp(\boldsymbol{w \cdot F(y,x)})}{Z_w(x)} \\ &= \arg \max_{y} exp(\boldsymbol{w \cdot F(y,x)}) \\ &= \arg \max_{y} \boldsymbol{w \cdot F(y,x)} \end{aligned}$$

于是，条件随机场的预测问题成为求非规范概率最大的最优路径问题：

$$\max_y (\boldsymbol{w \cdot F(y,x)})$$

这里路径表示标记序列，其中:

$$\begin{aligned} \boldsymbol{w} &= (w_1,w_2,\dots,w_K)^T \\ \boldsymbol{F(y,x)} &= (f_1(y,x),f_2(y,x),\dots,f_K(y,x))^T \\ f_k(y,x) &= \sum_{i=1}^n f_k(y_{i-1},y_i,x,i),\quad k = 1,2,\dots,K \end{aligned}$$

为了求解方便，考虑将优化问题写成如下形式：

$$\max_y \sum_{i=1}^n \boldsymbol{w} \cdot F_i(y_{i-1},y_i,x)$$

其中:

$$F_i(y_{i-1},y_i,x) = (f_1(y_{i-1},y_i,x,i),f_2(y_{i-1},y_i,x,i),\dots,f_K(y_{i-1},y_i,x,i))$$

是局部特征向量。下面给出维特比算法流程:

维特比算法：
输入:模型特征向量$\boldsymbol{F(y,x)}$,权值向量$\boldsymbol{w}$,观测序列$\boldsymbol{x} = (x_1,x_2,\dots,x_n)$
输出:最优路径$\boldsymbol{y^\ast = (y_1^\ast,y_2^\ast,\dots,y_n^\ast)}$

1. 初始化： $$\delta_1(j) = \boldsymbol{w} \cdot F_1(y_0 = start,y_1=j,x), \quad j = 1,2,\dots,m$$
2. 递推：对$i = 2,3,\dots,n$ $$\begin{aligned} \delta_i(l) &= \max_{1 \le j \le m}\{ \delta_{i-1}(j) + \boldsymbol{w} \cdot F_i(y_{i-1} = j,y_i = l,x)\},\quad l = 1,2,\dots,m \\ \varphi_i(l) &= \arg \max_{1 \leq j \leq m}\{ \delta_{i-1}(j) + \boldsymbol{w} \cdot F_i(y_{i-1} = j,y_i = l,x)\},\quad l = 1,2,\dots,m \end{aligned}$$
3. 终止: $$\begin{aligned} \max_y(\boldsymbol{w} \cdot \boldsymbol{F(x,y)}) &= \max_{1 \leq j \leq m} \delta_n(j) \\ y_n^\ast &= \arg \max_{1 \leq j \leq m} \delta_n(j) \end{aligned}$$
4. 回溯，得最优路径: $$y_i^\ast = \varphi_{i+1}(y_{i+1}^\ast),\quad i = n-1,n-2,\dots,1$$ 求得最优路径$\boldsymbol{y^\ast} = (y_1^\ast,y_2^\ast,\dots,y_n^\ast)$