线性判别分析

线性判别分析(LDA)是一种经典的线性学习方法，在二分类问题上最早由fisher提出，因此线性判别分析又称Fisher线性判别，该部分按照以下结构组织:

• LDA算法思想
• LDA算法推导
• 多分类任务

算法思想

LDA的思想非常朴素：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离，在对新的样本进行分类时，首先将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。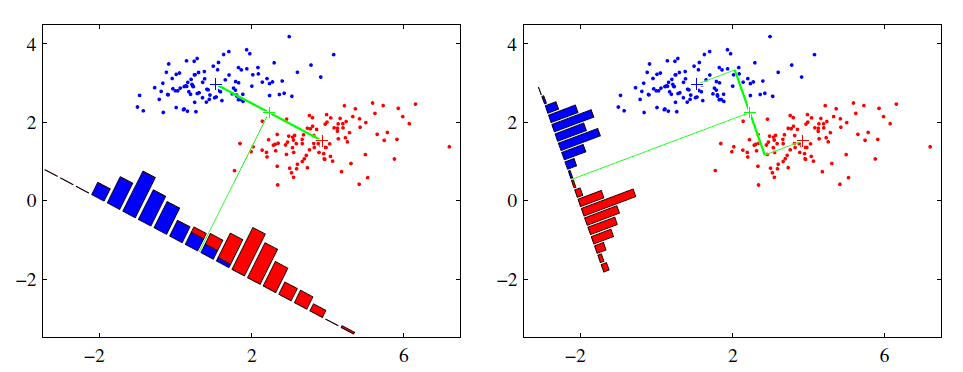

理论推导

投影方向求解

假设共有$N$个样本点$x_1,x_2,\dots,x_N$,其中有$N_1$个样本属于类别1，$N_2$个样本属于类别2，$N_1 + N_2 = N$, 记第$i$类样本点的均值为$\mu_i$,协方差矩阵为$\Sigma_i$,则有：

$$\begin{aligned} \mu_i &= \frac{1}{N_i} \sum_{x_i \in \mathcal{C_i}} x_i \\ \Sigma_i &= \frac{1}{N_i} \sum_{x_i \in \mathcal{C_i}} (x_i - \mu_i)(x_i - \mu_i)^T \end{aligned}$$

当将这些样本点向$w$投影后，投影后得到的点为$\tilde{x}_i = w^T x$,记此时类别$i$的均值为$\tilde{\mu}_i$,方差为$\sigma^2_i$,由均值方差计算公式可得:

$$\begin{aligned} \tilde{\mu}_i &= \frac{1}{N_i} \sum_{x_i \in \mathcal{C_i}} \tilde{x}_i = w^T \frac{1}{N} \sum_{x_i \in \mathcal{C_i}} x_i = w^T \mu_i \\ \sigma^2_i &= \frac{1}{N_i} \sum_{x_i \in \mathcal{C_i}}(\tilde{x}_i - \tilde{\mu }_i)^2 = \frac{1}{N_i} \sum_{x_i \in \mathcal{C_i}} (w^T x_i - w^T \mu_i)^2 \\ &= w^T [\frac{1}{N_i} \sum_{x_i \in \mathcal{C_i}} (x_i - \mu_i)(x_i - \mu_i)^T] w \\ &= w^T \Sigma_i w \end{aligned}$$

LDA有两个目标，一个是同类的点投影后尽可能接近，另一个目标则是不同类的点尽可能远离：

• 第一个目标我们通过投影后各类点的方差来进行刻画，使同类点的方差尽可能小: $$\min \quad w^T \Sigma_1 w + w^T \Sigma_2 w$$
• 第二个目标通过不同类的均值尽可能远来进行刻画,使不同类的均值尽可能远: $$\max \quad (w^T \mu_1 - w^T \mu_2)^2 = w^T (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T w$$

这两个目标可以通过一个目标函数来刻画：

$$\max \quad \frac{w^T (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T w}{w^T \Sigma_1 w + w^T \Sigma_2 w }$$

下面做如下标记,记$S_w = \Sigma_1 + \Sigma_2$为类内离散度矩阵，记$S_b = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T$ 为类间离散度矩阵，由此便得目标函数形式为:

$$\max \quad \frac{w^T S_b w}{w^T S_w w}$$

这是一个广义瑞利熵形式的优化问题，因为分子分母均是$w$的二次项，因此该优化问题的解仅与$w$的方向有关(因为用$cw$ 替代$w$并不影响目标函数的值)，不失一般性，可以限制$w^T S_w w = 1$，上述优化问题可以写为:

$$\max \quad w^T S_b w \quad s.t. \quad w^T S_w w = 1$$

该优化问题可以通过拉格朗日乘子法来进行求解,首先写出拉格朗日函数：

$$L(w,\lambda) = w^T S_b w - \lambda (w^T S_w w - 1)$$

上式对$w$求导可得:

$$\frac{\partial L(w, \lambda)}{\partial w} = S_b w - \lambda S_w w$$

令偏导等于0，可得$w$应当满足条件:

$$S_b w = \lambda S_w w$$

其中$S_b w = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^Tw = c(u_1 - u_2)$,又因为前面讨论过优化目标的取值仅仅与$w$的方向有关，因此不妨取$c = \lambda$,可得:

$$\mu_1 - \mu_2 = S_w w$$

因此可得最终$w$最优取值:

$$w^\ast = S_w^{-1}(\mu_1 - \mu_2)$$

这里需要说明一下，因为从前面我们可以推出这样一个表达式$S_w^{-1} S_b w = \lambda w$,这说明$w$应当是矩阵$S_w^{-1} S_b$的特征值，目标函数最大值应当是该矩阵的最大的特征值，最优$w$应当是该最大特征值所对应的特征向量，但后面求解为何没有没有从这个角度入手，这是该问题的特殊性，为解释这一点，首先看$S_b$表达式:

$$S_b = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T$$

这说明矩阵$S_b$的秩等于1($\mu_1 \neq \mu_2$),所以$S_w^{-1}S_b$秩也为1，这说明该矩阵有且仅有一个大于0的特征值，前面的推导相当于是构造性的给出了该最大特征值及对应特征向量表达式,将$w^\ast$代入$S_w^{-1}S_b w$:

$$\begin{aligned} S_w^{-1} S_b w^\ast &= S_w^{-1} (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T S_w^{-1}(\mu_1 - \mu_2) \\ &= C S_w^{-1}(\mu_1 -\mu_2) \end{aligned}$$

其中$C = (\mu_1 - \mu_2)^TS_w^{-1}(\mu_1 - \mu_2) >0 $($S_w$对称且可逆，推出其正定)，这说明$S_w^{-1}S_b$的最大特征值就是$C$,对应的特征向量刚好是$w^\ast$!
考虑到数值的稳定性，在实践中往往会首先对$S_w$进行特征值分解$S_w = U \Sigma U^T$,然后再求逆。

在线分类

在得到最佳投影向量后，需要设定一个策略，来对新来的样本进行分类，该策略选择通常有以下几种:

• 设定阈值，阈值选择通常有以下两种:
  • 均值取平均 $$t = \frac{\tilde{\mu}_1 + \tilde{\mu}_2}{2}$$
  • 根据样本点个数进行加权 $$t = \frac{N_2 \tilde{\mu}_1 + N_1 \tilde{\mu}_2}{N_1 + N_2}$$
• 在一维上估计概率密度函数，用Bayes决策方法分类

  多分类任务

  LDA 也可以推广到多分类任务中，假定存在$N$类，且第$i$类的样本数为$m_i$,首先定义全局散度矩阵: $$S_t = S_w + S_b = \sum_{i=1}^m(x_i - \mu)(x_i - \mu)^T$$ 其中$\mu$ 是所有样本点的均值，将类内离散度矩阵定义为每个类别的离散度矩阵之和: $$S_w = \sum_{i=1}^N S_{w_i}, \quad S_{w_i} = \sum_{x \in \mathcal{X_i}} (x - \mu_i)(x - \mu_i)^T$$ 然后求出类间离散度矩阵表达式: $$S_b = S_t -S_w = \sum_{i=1}^N m_i(\mu_i - \mu)(\mu_i - \mu)^T$$ 优化目标函数可以写成: $$\max_{W} \frac{tr(W^T S_b W)}{tr(W^T S_w W)}$$ 该问题的求导与前面一样，同样根据$W$的尺度不变性将上述优化问题转化为： $$\max_{W} \quad tr(W^T S_b W) \quad s.t. tr(W^T S_w W) = 1$$ 应用拉格朗日乘子法，并对$W$求导令导数为0可得: $$S_b W = \lambda S_w W$$ $W$的闭式解则是$S_w^{-1} S_b$的$d’$个最大非零广义特征值所对应的特征向量组成的矩阵，需要注意的是最终降的维数应当满足$d’ \leq N-1$,这是因为矩阵$S_b$本身最大只有$N-1$维，因此$S_w^{-1}S_b$至多有$N-1$个非零特征值。
  若将$W$视为一个投影矩阵，则多分类LDA相当于将样本投影到$d’$空间，$d’$通常远小于数据原有的属性数$d$,于是可以通过这个投影来达到讲维的目的，同时这个过程中也应用了类别的信息，因此$LDA$也常被视为一种经典的监督降维技术。