SVM补充

之前章节关于支持向量机的介绍已经比较详细了，最近发现有一些部分细节理解差一些意思，同时少了一部分内容，今天就在这里补充下，该部分章节按照以下结构组织:

• 优化问题等价
• 从硬间隔svm到软间隔svm
• svm应用于多分类问题
• 支持向量回归svr

  优化问题等价

  在求解优化问题时，我们往往考虑会将优化问题进行等价转换，以使得优化问题的求解更加容易，在进行极大似然估计时我们转化为求解对数似然函数极大就是一个典型的例子。这部分就系统的总结一下如何进行优化问题的等价转换,这里首先给出等价优化问题的定义:

  等价优化问题: 对于两个优化问题，如果从一个优化问题的解可以很容易得到另一个优化问题的解，反之亦然，则称两个优化问题是等价的。

一般优化问题的形式为:

$$\begin{aligned} &\min \quad f_0(x) \\ & \ s.t. \quad f_i(x) \leq 0,i=1,2,\dots,m \\ & \qquad \ \; h_i(x) = 0 , i =1,2,\dots, p \end{aligned}$$

下面给出将其转化为一个等价优化问题的几种转化思路。

变量替换

假设存在函数$\phi: R^n \rightarrow R^n$, 并且是一个双射(one-map-one),同时该函数的值域可以覆盖原优化问题的定义域$\mathcal{D}$，即$\mathcal{D} \subseteq \phi(\rm{dom} \phi)$,此时定义函数$\tilde{f}_i, \tilde{h}_i$:

$$\tilde{f}_{i}(z)=f_{i}(\phi(z)), \quad i=0, \ldots, m, \quad \tilde{h}_{i}(z)=h_{i}(\phi(z)), \quad i=1, \ldots, p$$

则可以得到优化问题:

$$\begin{array}{ll} \operatorname{minimize} & \tilde{f}_{0}(z) \\ \text { subject to } & \tilde{f}_{i}(z) \leq 0, \quad i=1, \ldots, m \\ & \tilde{h}_{i}(z)=0, \quad i=1, \ldots, p \end{array}$$

$x$与$z$之间的关系为$x = \phi(z)$, 假设$x$是原始优化问题的解，则$z = \phi^{-1}(x)$便是上述优化问题的解，同理，如果$z$是上述优化问题的解，则$x = \phi(z)$就是原始优化问题的解。

转换优化目标函数和约束函数

假设存在函数$\psi0:\mathbf{R} \rightarrow \mathbf{R}$是单调递增的，同时存在函数$\psi_1, \psi_2, \dots, \psi_m: \mathbf{R} \rightarrow \mathbf{R}$ 满足$\psi_i(\mu) \leq 0$当且仅当$\mu \leq 0$; 并且存在$\psi{m+1}, \psi{m+2}, \dots, \psi{m+p}: \mathbf{R} \rightarrow \mathbf{R}$满足$\psi_i(\mu) = 0$当且仅当$\mu = 0$。定义函数$\tilde{f}_i, \tilde{h}_i$如下:

$$\tilde{f}_{i}(x)=\psi_{i}\left(f_{i}(x)\right), \quad i=0, \ldots, m, \quad \tilde{h}_{i}(x)=\psi_{m+i}\left(h_{i}(x)\right)$$

变换后的优化问题表示为:

$$\begin{array}{ll} \operatorname{minimize} & \tilde{f}_{0}(x) \\ \text { subject to } & \tilde{f}_{i}(x) \leq 0, \quad i=1, \ldots, m \\ & \tilde{h}_{i}(x)=0, \quad i=1, \ldots, p \end{array}$$

该优化问题与原始优化问题是一致的，实际上，该优化问题与原始优化问题有着相同的可行集和最优解，在求解极大似然函数时我们转化为求解对数似然函数极大便是这样的等价思路。

引入松弛变量

在进行优化时我们往往更加喜欢等式约束，求解更加容易，对于不等式约束:

$$f_i(x) \leq 0, i = 1,2,\dots,m$$

可以考虑引入松弛变量$s_i$，将上述约束等价为下面的约束条件:

$$\begin{aligned} f_i(x) + s_i &= 0， i= 1, 2, \dots, m \\ s_i &\geq 0，i = 1,2,\dots, m \end{aligned}$$

通过引入松弛变量，将$m$个一般的不等式约束转化为$m$个等式约束和$m$个非负约束，使得求解更加容易。同时在某些情况下引入松弛变量可以起到放松约束，增大可行域范围的作用，比如在SVM中，原始的不等式约束为:

$$y_i w^T x_i \geq 1$$

通过引入松弛变量$\xi_i$,可以将上述不等式约束放松为:

$$\begin{aligned} y_i w^T x_i &\geq 1 - \xi_i \\ \xi_i & \geq 0, i = 1,2, \dots, N \end{aligned}$$

这样就拓宽了可行域，使得算法容许存在在支撑超平面之内的点，导出了软间隔支持向量机算法。

消除等式约束

这种等价思路是这样的，对于某些等式约束，我们可以闭式的构造出函数$\phi(z)$，使得等式约束可以得到固有满足$f_i(\phi(z)) = 0$,由此便可得到等价的优化问题:

$$\begin{array}{ll} \text { minimize } & \tilde{f}_{0}(z)=f_{0}(\phi(z)) \\ \text { subject to } & \tilde{f}_{i}(z)=f_{i}(\phi(z)) \leq 0 \end{array}$$

对于凸优化问题，等式约束都是线性约束，等式约束记为$A x = b$，假设存在矩阵$F \in \mathbf{R}^{n \times k}$满足$\mathcal{R}(F) = \mathbf{N}(A)$，那么假设我们有原始等式约束的一个可行解$x_0$，那么所有满足等式约束的解都可以写成如下形式:

$$x = Fz + x_0$$

对于这样的$x$，等式约束是固有满足的，因此就将原始优化问题转化为:

$$\begin{array}{ll} \operatorname{minimize} & f_{0}\left(F z+x_{0}\right) \\ \text { subject to } & f_{i}\left(F z+x_{0}\right) \leq 0, \quad i=1, \ldots, m \end{array}$$

从硬间隔SVM到软间隔SVM

在之前介绍从硬间隔SVM到软间隔SVM时，更多地是从几何直观角度，直接引入了松弛变量导出了软间隔SVM的形式，今天这部分以更加细致的角度来介绍这一转化过程。

如果将SVM原始优化问题转化为无约束优化问题，则可以写做:

$$\min_{w, b} \frac{1}{2} ||w||^2 + \sum_{i=1}^N l_{0-\infty} (y_i (w^T x_i + b))$$

其中:

$$l_{0-\infty} (b) = \begin{cases} \infty & if \ b < 0 \\ 0 & if \ b > 0 \end{cases}$$

这样的惩罚项相当于是对于不满足约束的样本零容忍，只要不满足约束，则施加一个$\infty$的惩罚，现在我们期望将惩罚系数放松一下，即便存在不满足约束的点，仍然可以进行优化，那么惩罚函数最直接想到的便是$l_{0-1}$:

$$l_{0-1}(b) = \begin{cases} 1 & if \ b < 0 \\ 0 & if \ b > 0 \end{cases}$$

但采用这样一个惩罚函数会导致优化问题非凸，而我们是期望求解一个凸优化问题的，因此便考虑$l{0-1}$的凸近似，常用的凸近似有$l{lin}$和$l{quad}$,如下图所示: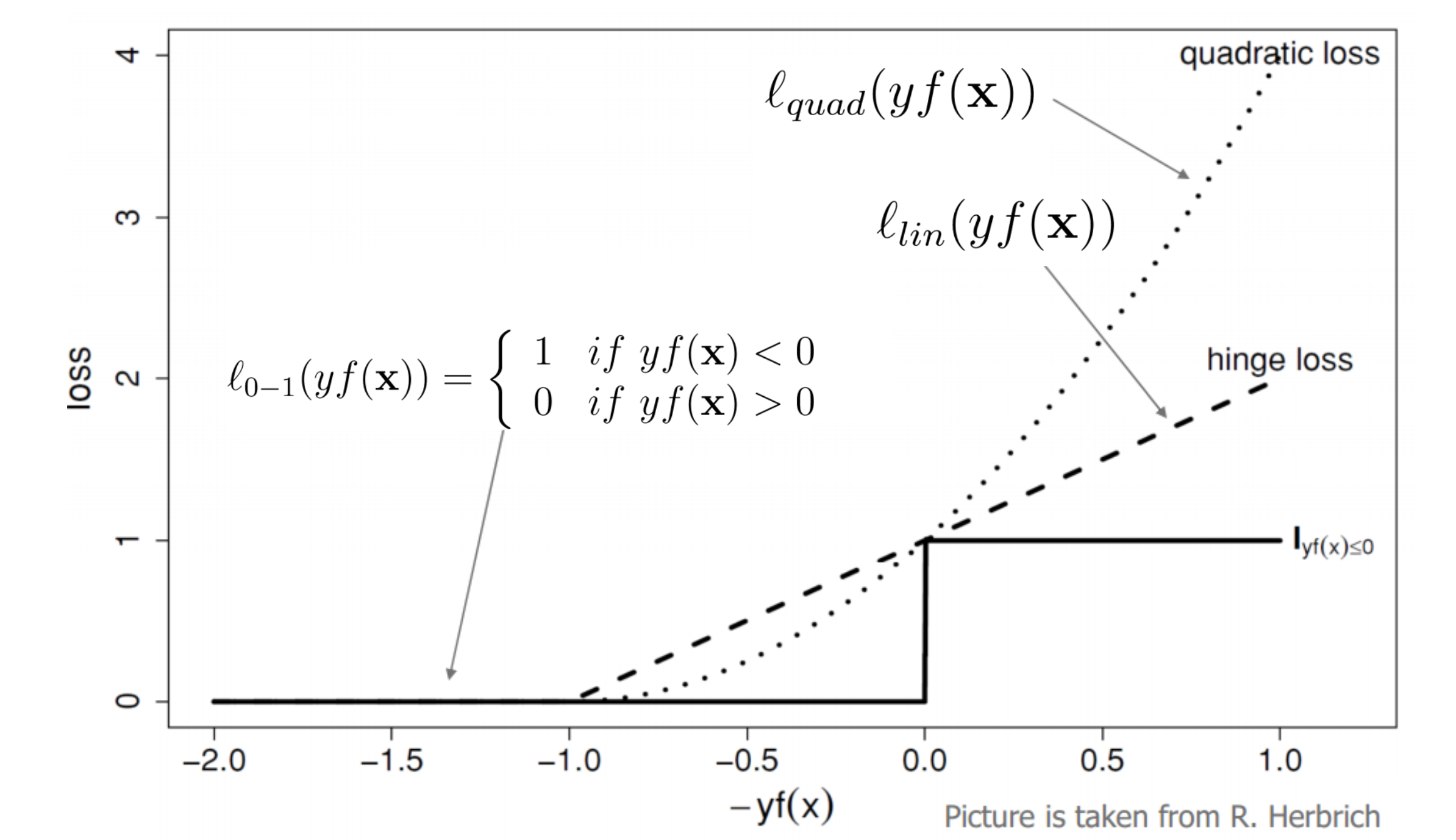

若记$f(x) = w^T x + b$，则$l{lin}$和$l_{quad}$在该问题中的表达式为:

$$\begin{aligned} l_{lin}(yf(x)) &= \max(0, 1 - yf(x)) \\ l_{quad}(yf(x)) &= \max(0, (1-yf(x))^2) \end{aligned}$$

可以看到，第一个损失函数是分段线性的，也被称为合页损失,凸函数，不光滑；第二个损失函数也是凸函数，且光滑。
因此此时目标函数可以写做:

$$\min_{w,b} \quad \frac{1}{2} ||w||^2 + \sum_{i=1}^N \xi_i$$

其中$\xi_i = \max(0, 1- y_i f(x_i))$， 该优化问题等价于:

$$\begin{array}{ll} \min &\frac{1}{2} ||w||^2 + \sum_{i=1}^N \xi_i \\ s.t. & y_i f(x_i) \geq 1 - \xi_i, i = 1,2,\dots, N \\ & \xi_i \geq 0, i =1,2,\dots, N \end{array}$$

这便是我们熟悉的软间隔支持向量机原始优化问题的形式。

SVM应用于多分类问题

SVM最常用的场景是二分类场景，但这并不意味着SVM不能应用于多分类问题，将SVM应用于多分类问题有如下几个解决思路:

• 训练多个$one \ vs \ all$分类器
• 训练多个$one \ vs \ one$分类器
• 训练一个联合分类器

下面就分别讲解下这三种实现多分类器构建的思路。

训练多个$one \ vs \ all$分类器

思路也是简单的，有$k$个类别我就训练$k$个分类器，在第$i$个分类器训练时将第$i$类样本看作一类，将剩余的其他样本看作另一类。

采用这种思路容易碰到两个问题:

• $k$个分类器的超平面参数$(w_k, b_k)$未必在一个尺度下，因为将$w_k$和$b_k$同时放大或者缩小$d$倍并不影响该超平面的分类结果，但会导致$w_k^T x + b_k$成倍放大或缩小。
• 在模型学习时因为是$one \ vs \ all$，就会导致正负样本数不平衡，使得分类器不能得到充分训练。

训练多个 $one \ vs \ one$分类器

在这种思路下，共需要训练$\frac{k(k-1)}{2}$个分类器，在进行决策时通过投票的方式决定将一个样本划分为哪一类。

这种思路存在的问题主要有:

• 随着类别数目的增多，需要训练的分类器的数量是以$k^2$的速度增长的。
• 基于投票进行决策经常会出现冲突。

训练一个联合分类器

前面两种解决思路都是分开训练多个超平面参数然后再联合起来决策，但其实也可以在一个优化问题求解中将多个超平面参数同时学出来，其实本质上就是$one \ vs \ all$思路,优化问题可以写做:

$$\begin{array}{ll} \min_{w,b} & \frac{1}{2} \sum_{y} ||w_y||^2 + C \sum_{i=1}^N \sum_{y \neq y_i} \xi_{iy} \\ s.t. & w_{y_i}^T x_i + b_{y_i} \geq w_y^T x_i + b_y + 1 -\xi_{iy}, \forall i,\forall y \neq y_i \\ & \xi_{iy} \geq 0, \forall i,\forall y \neq y_i \end{array}$$

在进行决策时:

$$\hat{y} = \argmax_{k} (w_k^T x + b_k)$$

支持向量回归(SVR)

支持向量机的思路也可以用于回归问题上，对于样本$(x,y)$,传统的回归模型通常直接基于模型输出$f(x)$与真实输出$y$之间的差别来计算损失，当且仅当$f(x)$与$y$完全相同时损失才为0。与此不同，支持向量回归假设我们能够容忍$f(x)$与$y$之间最多有$\epsilon$的偏差，即仅当$f(x)$与$y$之间的差别绝对值大于$\epsilon$时才计算损失，如下图所示。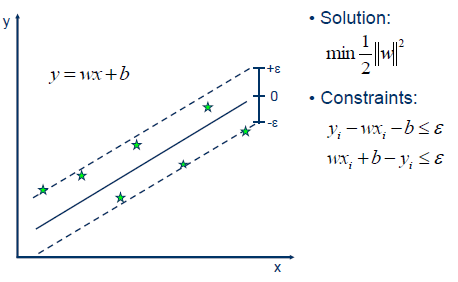

我们期望$\epsilon$能够尽可能小，同时希望在误差带不变大的情况下能够包含尽可能多的样本点，也就是希望几何间隔能够尽可能大一些，也就是说我们期望在函数间隔尽可能小的情况下几何间隔能够尽可能大，根据几何间隔与函数间隔的关系:

$$gap_{geo} = \frac{gap_{func}}{||w||}$$

因此SVR问题可形式化为:

$$\min_{w,b} \frac{1}{2} ||w||^2 + C \sum_{i=1}^m l_{\epsilon} (f(x_i) - y_i)$$

其中$C$为正则化常数，$l_\epsilon$表示为:

$$l_\epsilon(z) = \begin{cases} 0, & if |z| \leq 0 \\ |z| - \epsilon, & otherwise \end{cases}$$

在进行回归时，往往会存在一些离群点，此时这些点我们并不期望它们出现在$2 \epsilon$之内，因此考虑引入两个松弛变量，将优化问题转化为:

$$\begin{array}{ll} \min_{w,b,\xi_i,\hat{\xi}_i} \frac{1}{2} &||w||^2 + C \sum_{i=1}^n (\xi_i + \hat{\xi}_i) \\ s.t. & f(x_i) - y_i \leq \epsilon + \xi_i \\ & y_i - f(x_i) \leq \epsilon + \hat{\xi}_i \\ & \xi_i \geq 0, \hat{\xi}_i \geq 0 \end{array}$$

后面求解也是转为对偶问题进行求解，同时因为优化问题的独特形式，使得最终进行回归时只会计算样本点之间的点积，因此可以很方便地引入核技巧，完成非线性回归任务。